简易超人函数

引子

2011年网间热传一张名为“蝙蝠侠函数”（或叫蝙蝠侠等式）的截图。

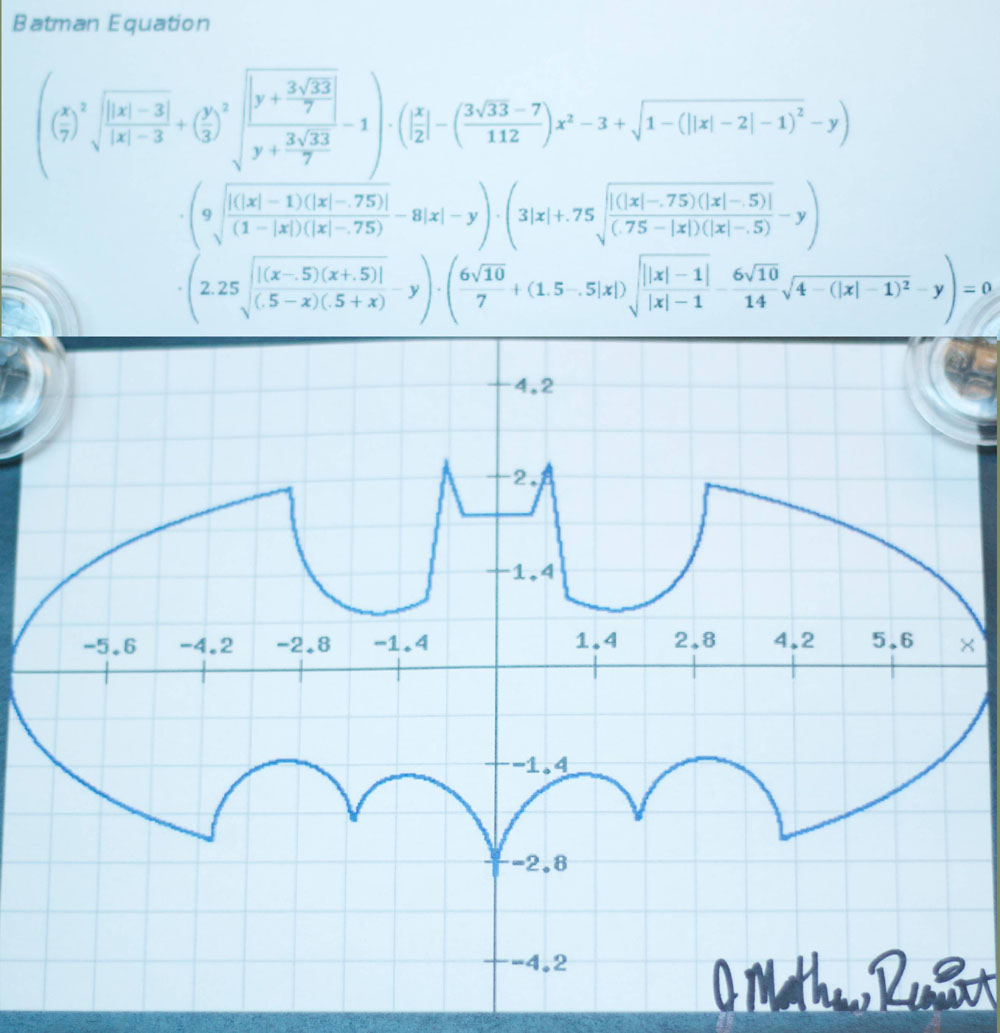
the hitting batman curve shot

自然会有同学疑问有没有类似的“超人”函数呢？时至2013年，WolframAlpha给出了自己的答案：可以，并且我们还能做的更多。

函数式

本式主要由WolframAlpha的superman insignia演算得出，感谢WolframAlpha团队的贡献！

superman piecewise function explained

LaTex格式文本

\begin{cases} 
  18/5 & \left|x\right|<7.395 \\
  -643\operatorname{abs}(x)/500+1311/100 & 7.395<\left|x\right|<10.197 \\
  114\operatorname{abs}(x)/125-93/10 & \left|x\right|<10.197 \\
  91\operatorname{abs}(x)/100-391/50 & -1.53<x<1.053 \\
  -\cos(1/4-x/2)-59/10 & -1.53<x<1.053 \\
  -19/5 & -4.418<x<-3.011 \\
  -\cos(37/100-x/2)-41/10 & -3.011<x<2.522 \\
  19.1x-112.5 & 5.948<x<6 \\
  21/10 & 3.909<x<6 \\
  +17/8\cos(5/56\pi(x-7/5))+12/25 & 3.909<x<5.948 \\
  21/10 & -6.953<x<-6.12 \\
  32x/25+11 & -8.594<x<-6.953 \\
  -91x/100-391/50 & -8.594<x<-7.8 \\
  2/25(25\cos^{-1}\left(-x/2-29/10)-9\right) & -8.594<x<-6.12 \\
  0 & 5.6<x<7.1 \\
  19.1x-133.7 & 7<x<7.1 \\
  \frac{17\cos(5\pi x/56)}{8} & -3.599<x<5.6 \\
  \frac{-32x+275}{25} & 7.1<x<8.586 \\
  -2e^{\left(\frac{5}{256}\left(20x-139\right)\right)}+\frac{1}{2} & -3.162<x<6.947 \\
  -2/37(-5\cos^{-1}\left(\frac{5x}{3}+\frac{16}{3}\right)-1) & x<-3.162 \\
  -2/37(-10\pi+5\cos^{-1}\left(\frac{5x}{3}+\frac{16}{3}\right)-1) & x<-3.599 \\
  \frac{91x-782}{100} & 6.947<x<8.586 \\
  \frac{-91x-782}{100} & -5.886<x<-4.418 \\
  \frac{7\sqrt{\left|\log\left(\frac{571}{100}-\frac{6x}{5}\right)\right|}-32}{10} & -5.886<x<3.915 \\
  1/154(-200\pi\cdot1-100\cos^{-1}\left(x-3\right)+107) & x>2.522 \\
  1/154(-200\pi\cdot1+100\cos^{-1}\left(x-3\right)+107) & x> 3.928
\end{cases}